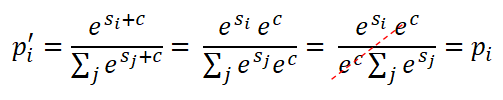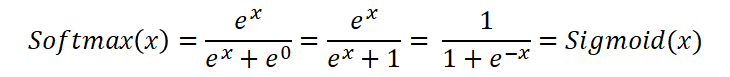What is the Softmax function?
In this article, we will review the Softmax function and its role in neural networks. It is typically used in the output layer of a multi-class classification neural network to predict the class label for a given input.
The outline of the article is as follows. We begin by motivating the need for the softmax function in neural networks. We then review some alternatives, like the Linear and Sigmoid functions and vector normalization and why they don’t work for the intended purpose. We then detail the Softmax function and outline some of its properties. Finally, we conclude by relating it to the original goal of multi-class classification.
Table of contents
Motivation: why do we need the Softmax function
The multi-class classification problem entails assigning a class label to a given input among more than 2 possible classes (which is referred to as Binary classification). Machine learning models achieve this by estimating the probabilities for each of the classes being the correct label for the input. The label with the highest probability is then chosen as the prediction. Thus, a deep learning neural network, must also output probabilities for each of the class labels.
The need of a dedicated output layer in neural networks arises because typically, the training process causes the penultimate layer to produce real-valued raw outputs of arbitrary scale. They are not guaranteed to be probabilities and therefore not well-suited for making predictions.
Like any layer, the output layer also consists of nodes. The standard approach is to have one node for each of the classes. Thus, if there are k potential classes, then the output layer of the classification neural network will also have k nodes.
The activation function, by definition, decides the output of a node in the neural network. The output layer of a multiclass classification neural network therefore must use an activation function that satisfies the following properties.
- Each node must output a probability between 0 and 1, which can then be interpreted as the probability of the input belonging to the corresponding class.
- The sum of the outputs of all the nodes must be 1. This ensures that we account for all the classes that the input may belong to.
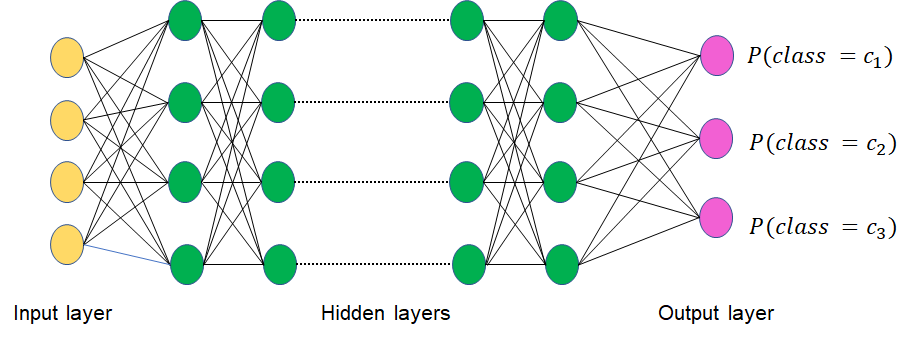 |
| Fig. 1: A multi-class classification neural network, with k=3. |
Fig. 1 illustrates these requirements for a 3-class neural network. The input layer, shown in yellow depends on the specific input. There are several hidden layers in green that transform the inputs to output layer, a vector of 3 probability values. The label corresponding to the highest value is the predicted class. The raw output of the penultimate neural network layer is not a valid probability vector. In the case of convolutional neural networks, which are commonly used for image classification, the hidden layers perform convolutions and a dedicated output layer estimates the probabilities. Other neural network architectures also employ a similar output layer.
Alternatives to Softmax function and why they don’t work
Given the above requirements for the activation, we will consider some alternative linear and non-linear activation functions in neural networks and learn why they don’t work for the output layer of multi-class classification neural networks.
- The Linear Activation Function is the identity function: the output is the same as the input. The output layer may receive arbitrary inputs, including negative values, from the hidden layers. A weighted sum of such inputs will never satisfy the above requirements. Therefore, the linear activation function is not a good choice for the output layer.
- The sigmoid activation function, uses the S-shaped logistic function to scale the output to values between 0 and 1. This does satisfy the first requirement, but has the following problems. The values of each of the k nodes are independently calculated. Therefore, we cannot ensure that the second requirement is met. Moreover, values close to each other get squished by the nonlinear nature of the logistic function. The sigmoid activation function is ideally suited for binary classification, where there is only one output (the probability of one class) and the decision threshold can be tuned using an RoC curve. Logistic regression for binary classifiers uses this approach. It should also be noted that the hyperbolic tangent, tanh function is also a logistic function and has the same issues with being used in the output layer of the network.
- Standard normalization involves dividing the input for a node by the sum of all inputs to get the output of the node. For example, in Fig. 1, say the weighted average of the inputs to the three pink output nodes are s1, s2 and s3 respectively. The respective outputs of the three nodes with standard normalization will be as follows.
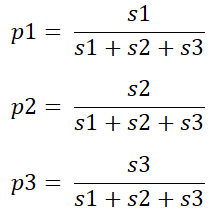
It can be easily verified that normalization ensures that both the above requirements are met. But there are two problems with this function. Firstly, standard normalization is not invariant with respect to constant offsets. In other words, adding a constant c to each of the inputs s1, s2 and s3 changes in the outputs significantly. Consider s1 = 0, s2 = 2 and s3 = 4. This results in p1 = 0, p2 = 1/3 and p3 = 2/3. Let us consider the case when s1, s2 and s3 are scaled by 100: s1 = 0, s2 = 102, and s3 = 104. This could happen due to various reasons, like a scaled version of the input, or the model parameters. The resulting probabilities are p1 = 0, p2 = 0.4951, and p3 = 0.5048. The relative difference between the probabilities reduced proportionally to the constant offset. Secondly, if the input to the node is 0, which is the case for the first node, the output probability is also 0. In certain applications, it may be needed to map a 0 input to a small, but non-0 probability. Note that negative values are problematic with standard normalization.
Softmax Activation
The softmax activation for the node i is defined as follows.
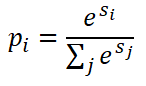
Each of the k nodes of the softmax layer of the multi-classification neural network will be activated using this function: s_i denotes the weighted average of the inputs to the ith node. All the inputs are passed through the exponential function and then normalized. The function converts the vector of inputs to the output layer of k nodes into a vector of k probabilities. Note that vector of inputs may contain negative values also.
In the above example, where s1 = 0, s2 = 2 and s3 = 4, the corresponding probabilities are computed as follows.
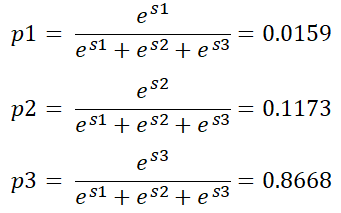
The output values are guaranteed to satisfy the above requirements: the values will be probabilities between 0 and 1. They will also sum to 1 by construction. Being a non-linear function, the resulting probability distribution tends to be skewed toward larger values: s2 and s3 differ by a factor of 2, but the corresponding p2 and p3 are significantly different.
Softmax function can be interpreted as multi-class logistic regression. The output vector of k probabilities represents a multinomial probability distribution, where each class represents a dimension of the distribution. Next, we review some properties of the softmax function.
Some Properties of the Softmax Activation Function
- The softmax function is invariant to constant offsets. As outlined above, the main problem with standard normalization is that the softmax function is not invariant to constant offsets. Softmax function, on the other hand, produces the same output when the weight average inputs to the nodes are changed by a constant value.
- The softmax activation and Sigmoid functions are closely related. Specifically, we get the sigmoid function when we have two inputs to the Softmax activation and one of them is set to 0. In the derivation below, we send a vector [x, 0] into the softmax function. The first output is the sigmoid function.
- Relation with argmax: The argmax function returns the index of the maximum element from a list of numbers. It can be used to predict the class label based on the vector of probabilities output by the softmax layer. It can also be used as an activation function inside the neural network. Unfortunately, the argmax function is not differentiable and therefore cannot be used for the training process. The softmax is a differentiable function and therefore enables the learning process. The softmax function can be interpreted as a soft approximation of the argmax function, which makes a hard decision by picking up the index. The softmax function, on the other hand, would assign a probability proportional to the input’s rank. The probability could be used to make a soft decision, instead of making a hard choice of an index.
- Derivatives of the softmax function. Let us look at the derivative of the softmax function. We will first consider the partial derivative function of p_i with respect to s_i. It can be derived from elementary calculus as follows.
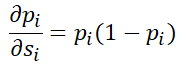
This derivative is maximized when p_i is 0.5 and there is maximum uncertainty. If the neural network is highly confident, with p_i being close to 0 or 1, the derivative goes to 0. The interpretation is as follows. If the probability associated with the class i is already very high, then a small change in the input will not significantly alter the probability, thereby making the output value robust to small changes in the input.
Next, we look at the partial derivative function with respect to s_j, the other cross-entries of the input vector.
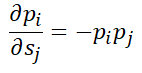
This derivative is maximized when both p_i and p_j are 0.5. This occurs when all the other labels of the multi-class classification problem have 0 probability and the model is trying to choose between 2 classes. Moreover, the negative sign implies that the confidence in class label i decreases as the weighted input to s_j increases.
Role in Multi-Class Classification
Next, we close the loop on the end-goal: multi-class classification using neural networks. The neural network weights are tuned by minimizing a loss function. The softmax activation function enables this process as follows.
Let’s consider the case of 3 classes, as shown in Fig. 1. Instead of labeling the input values categorically as c1, c2 and c3, we use one-hot encoding to assign the labels: class c1 becomes [1,0,0], c2 becomes [0, 1, 0] and c3 becomes [0, 0, 1]. Given that our neural network has an output layer of 3 nodes, these labels translate to the optimal output vectors for the input arrays. An input that belongs to class c3, must produce the expected output vector [0, 0, 1].
Let’s take the example from above, where the softmax-activated output layer produced the output [0.0159, 0.1173, 0.8668] as shown above. The error between the expected and the predicted output vectors is quantified using the cross-entropy loss function and it is used to update the network weights.
Conclusion
In this article we reviewed the need for an appropriate activation function for the output layer of a multi-class classification deep learning model. We then outlined why alternative mathematical functions, such as the Sigmoid functions and the Tanh activation function do not work well. The Softmax activation function was then described in detail. The exponential operation, followed by normalization, ensures that the output layer produces a valid probability vector that can be used for predicting the class label. Given its properties, the softmax activation is one of the most popular choices for the output layer of neural network-based classifiers.
References
López, Osval Antonio Montesinos, et al. Multivariate Statistical Machine Learning Methods for Genomic Prediction. Springer Nature, 2022.
Saitoh, Koki. Deep Learning from the Basics: Python and Deep Learning: Theory and Implementation. Packt Publishing Ltd, 2021.
Sewak, Mohit, et al. Practical Convolutional Neural Networks: Implement Advanced Deep Learning Models Using Python. Packt Publishing Ltd, 2018.