Introduction
As the name would suggest, a sparse matrix is one whose elements have fewer nonzero values. Sparse matrices are encountered during machine learning and its application. It is very common to come across them in data, data preparation, and sub-fields of machine learning. Working with such matrices as though they are dense leads to wastage of resources in terms of time and space complexity.
This article talks about what sparse matrix and explains they are different from a dense matrix. You will get to know where sparse matrices are encountered, it’s advantages and disadvantages. We will talk about what is sparsity and the time, space complexity of working with these matrices. We will also go through python implementations of a couple different formats used while working with a sparse matrix.
Table of contents
Sparse Matrix
A matrix comprised of mostly non-zero values is a sparse matrix, in other words, it’s a matrix where majority elements are zero. Below is an example of such a matrix.
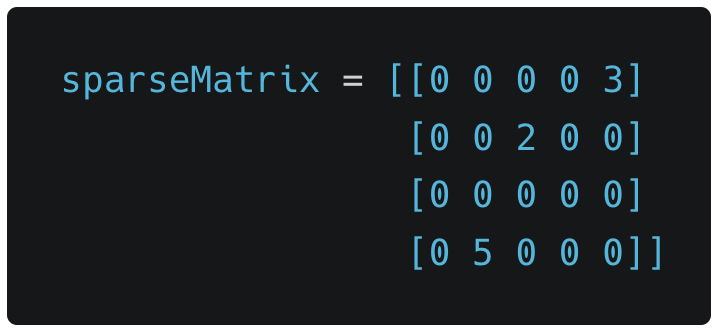
Dense Matrix
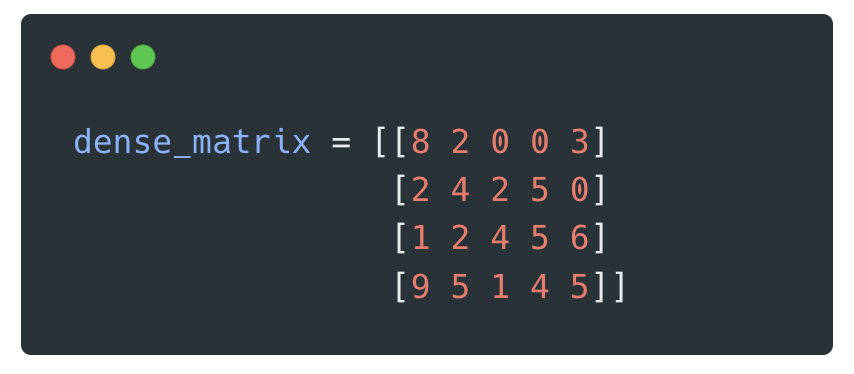
In contrast to the above matrix, a dense matrix comprises mostly non-zero elements. Below is an example of the same.
Sparsity
When working with a sparse matrix, one should talk in terms of the sparsity of that matrix.
Sparsity = (number of zero elements) / (matrix size)
We shall be looking at python commands to calculate this in later parts of the tutorial.
Problems with High Sparsity
Space Complexity
In practical scenarios, every large matrix is mostly made up of zeros. If we represent these matrices as though they are dense, although the non-zero elements are very less, it would require a lot of memory and hence lead to wastage of resources.
An example of a large matrix is when we try to represent purchases of people from a huge product catalog like Amazon in a matrix. Such a matrix would require a lot more space if we represent it as a dense matrix.
Time Complexity
Let’s assume that we have a large sparse matrix, and we try to do some computations like matrix multiplications with it. The bulk of the operations would be just addition/multiplication of zeros.
The execution cycle of the most basic algorithms would be dominated by just operating on 0s. This again would lead to wastage of resources and time.
Also Read: How to Use Pandas Melt – pd.melt() for AI and Machine Learning.
Sparse Matrices in Machine Learning
Sparse matrixes are encountered in a number of machine learning scenarios
Data
You can encounter sparse matrix in data of varying sizes. Examples of sparse matrix can be:
- Whether an article contains words from the complete dictionary.
- Whether a user has viewed products on Amazon.
- Whether a user has watched a movie from the Netflix movie catalog.
Data Preparation
There are different encoding systems employed for preparation of data. A few of them where we see high sparsity are:
- TF-IDF encoding (Term Frequency-Inverse document)
- Ex: Representing frequency scores of words in the vocabulary.
- Count encoding
- Ex: Representation of frequency of airplane travel in a year
- One-hot encoding
- Ex: Convert the categorical data to sparse binary vectors.
Areas of Study
In cases where input data is almost always sparse, we need to create specialized models to deal with them.
Few examples of these areas are:
- Using computer vision to work with photos that have a lot of black pixels.
- Natural language processing when working with documents of text.
- Building a recommender system in scenarios where the total items have high count, but a typical user just uses a subset of these items.
Working with Sparse matrix
In order to work with sparse matrix efficiently, we need to use alternate data structures to represent the non-zero values.
Sparse matrix formats can effectively be divided into 3 main categories. Let’s go through them one at a time.
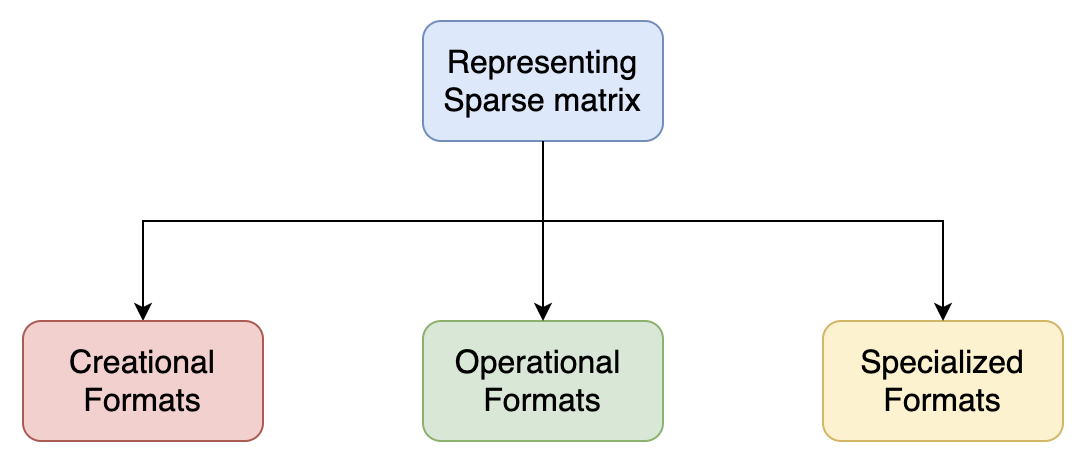
Creational Format
Dictionary Of Keys (DOK)
This format uses coordinates of the non-zero elements as keys to the map and the non-zero element as the value for that key.
The element access can be reduced to O(1) using hash map as the underlying data structure. The disadvantage here is that it is slow for arithmetic operations where one needs to loop over elements.
Coordinate format (COO)
Coordinate format stores non-zero elements as triplets. Tuples of row index, column index and data value are stored in 3 slices. Allowing the use of element (row[i], column[i]) = value[i].
Appending non-zero elements to the end of data is fast. The issue occurs with random reads, in which case O(n) time is required to get the value of an element. Sorting the values in COO response can improve the overall access time, but it would still not be that efficient.
Operational Formats
Compressed Sparse Row format (CSR)
This format is similar to COO above except that the row index slice is compressed.
The row index slice stores the cumulative count of non-zero elements in each row, such that row[i] contains the index into both column[] and data[] of the first non-zero element of the row [i].
Storage requirement is reduced and random access if faster. Update to the zero elements is relatively slow because, insertions would have to be done to the slices.
Compressed Sparse Column format (CSC)
This is identical to CSR except that the column index slice is compressed rather than the row index slice as with CSR. Under CSC format, values are stored in column major order and can be thought of as a natural transpose of CSR.
Specialized Formats
Diagonal format (DIA)
The diagonal Format is use used specially for symmetric diagonal matrix. A square matrix has an equal number of rows and columns. A symmetric diagonal matrix is a square matrix with non-zero elements only along its top left to bottom right diagonal. The diagonal format only stores the diagonal elements of the matrix.

Sparse Matrices in Python
SciPy, short for scientific python, is an open source python library. It provides the ability to visualize and manipulate data.
Start with declaring a NumPy array. We can call this the original matrix for now, as we can see it is a sparse matrix.

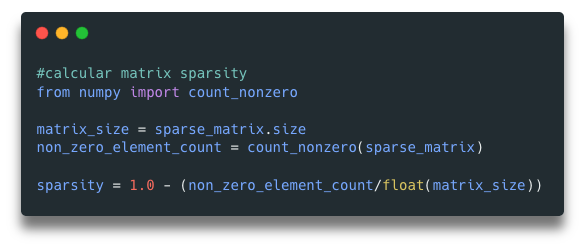
We can do operations like calculating sparsity of the matrix. Using SciPy, there is no method for directly calculating this, but usually people do 1 – (number_of_non_zero_elements / matrix_size).
SciPy has been written on top of NumPy and offers a fully-featured version of linear algebra, which is lacking in NumPy. Let’s check out a couple sparse matrix formats in python.
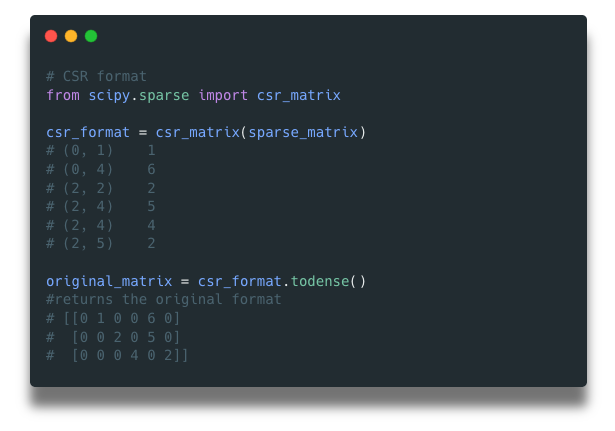
Using csr_matrix command to generate the CSR format for the matrix. The to_dense() command helps you convert back a format to the original matrix.
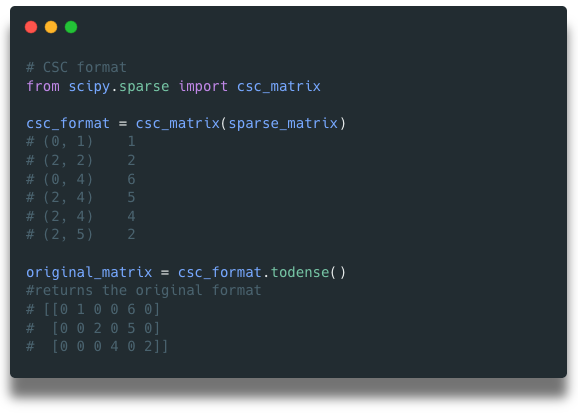
Using csc_matrix command to generate the CSC format for the matrix.
Extensions
You can take explore more about the topic by:
Checking out the official documentation on SciPy.
Exploring the implementation of other formats for spare matrices in python.
Also Read: What Are Word Embeddings?
Conclusion
This tutorial helps you explore sparse matrices in python and how to work with them using the SciPy package.
What we learned is:
You will get to know where sparse matrices are encountered, it’s advantages and disadvantages. We will talk about what is sparsity and the time, space complexity of working with it. We will also go through python implementations of working with a sparse matrix.
- The difference between a sparse and dense matrix within Matrix Data Structure.
- The issues one faces while working with these matrices.
- The different areas where it is likely to come across a sparse matrix.
- The ways to format sparse data and work with it efficiently
References
Brownlee, Jason. “A Gentle Introduction to Sparse Matrices for Machine Learning.” MachineLearningMastery.Com, 13 Mar. 2018, https://machinelearningmastery.com/sparse-matrices-for-machine-learning/. Accessed 22 Feb. 2023.
Contributors to Wikimedia projects. “Sparse Matrix.” Wikipedia, 11 Feb. 2023, https://en.wikipedia.org/wiki/Sparse_matrix. Accessed 22 Feb. 2023.
SciPy Sparse Data. https://www.w3schools.com/python/scipy/scipy_sparse_data.php. Accessed 22 Feb. 2023.
