Introduction
Joint distribution, also known as joint probability distribution, calculates the likelihood of two events occurring together and at the same point in time. Joint probability is the probability that two events can occur simultaneously. Probability is a branch of mathematics which deals with the occurrence of a random event. In simple words it is the likelihood of a certain event. This concept is used a lot in statistical analysis, but it can also be used in machine learning as a classification strategy to produce generative models.
Table of contents
Also Read: What is Argmax in Machine Learning?
What are Joint Distribution, Moment, and Variation?
Probability is very important in the field of data science. It is quantified as a number between 0 and 1 inclusive, where 0 indicates an impossible chance of occurrence and 1 denotes the certain outcome of an event. For example, the probability of drawing a red card from a deck of cards is 1/2 = 0.5. This means that there is an equal chance of drawing a red and drawing a black; since there are 52 cards in a deck, of which 26 are red and 26 are black, there is a 50-50 probability of drawing a red card versus a black card.
When creating algorithms data scientists will often need to come up with inferences based on statistics. This would then be used to help predict or analyze data better. Statistical inference refers to process that is used to find the properties that exist in a probability distribution. One such distribution is known as joint distribution or joint probability.
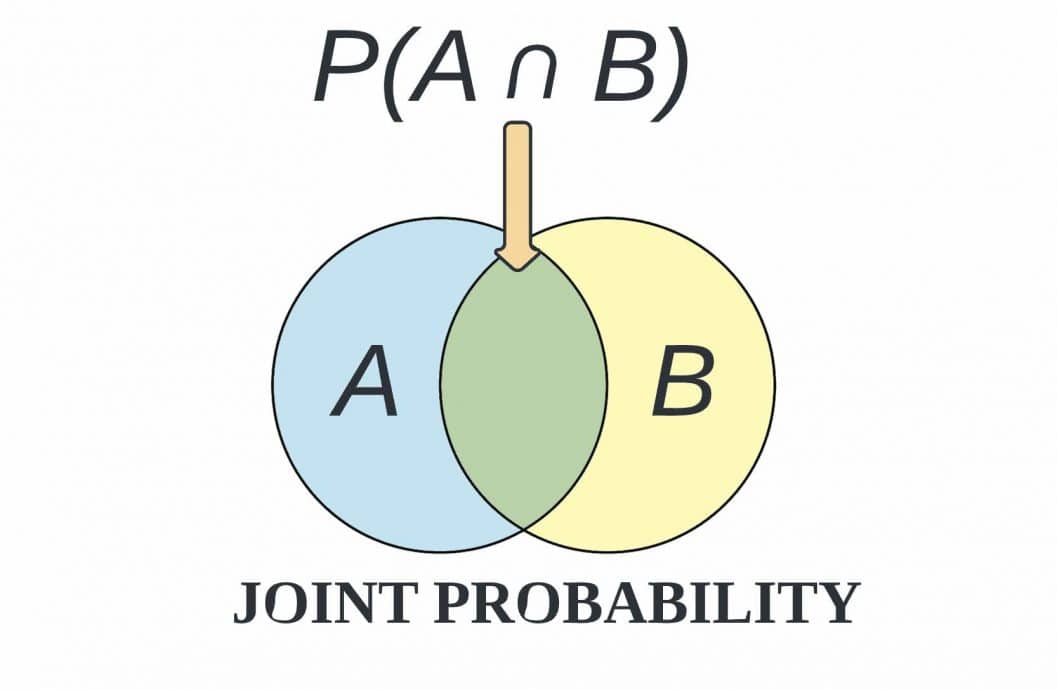
Joint probability can be defined as the chance that two or more events will occur at the same time. The two events are usually designated event A and event B. In probability terminology, it can be written as p(A and B). Hence, joint probability is the probability that two events can occur simultaneously.
Joint probability can also be described as the probability of the intersection or domain discrepancy of two or more events. This is written in statistics as p(A ∩ B). Joint distribution matching across subjects is used in machine learning to help identify a relationship that may or may not exist between two random variables. Joint probability distribution can only be applied to situations where more than one observation can occur at the same time.
For example, from a deck of 52 cards, the joint probability of picking up a card that is both red and 6 is P(6 ∩ red) = 2/52 = 1/26, since a deck of cards has two red sixes—the six of hearts and the six of diamonds.
Every now and then, in machine learning literature, the terms “first moment” and “second moment” will pop up. So what does moment refer to in the context of machine learning? In short, the first moment of a set of numbers is just the mean, or average, and the second moment is usually just the variance. The variance is the mean squared difference between each data point and the center of the distribution measured by the mean.
Suppose you have four numbers (x0, x1, x2, x3). The first raw moment is (x0^1 + x1^1 + x2^1 + x3^1) / 4 which is nothing more than the average. For example, if your four numbers are (2, 3, 6, 9) then the first raw moment is
(2^1 + 3^1 + 6^1 + 9^1) / 4 = (2 + 3 + 6 + 9) / 4 = 20/4 = 5.0
In other words, to compute the raw first moment of a set of numbers, you raise each number to 1, sum, then divide by the number of numbers. The second raw moment of a set of numbers is just like the first moment, except that instead of raising each number to 1, you raise to 2, also known as squaring the number.
Put another way, the second raw moment of four numbers is (x0^2 + x1^2 + x2^2 + x3^2) / 4. For (2, 3, 6, 9) the second raw moment is
(2^2 + 3^2 + 6^2 + 9^2) / 4 = (4 + 9 + 36 + 81) / 4 = 130/4 = 32.5.
In addition to the first and second raw moments, there’s also a central moment where before raising to a power, you subtract the mean.
For example, the second central moment of four numbers is [(x0-m)^2 + (x1-m)^2 + (x2-m)^2 + (x3-m)^2] / 4. For (2, 3, 6, 9), the second central moment is
[(2-5)^2 + (3-5)^2 + (6-5)^2 + (9-5)^2] / 4 = (9 + 4 + 1 + 16) / 4 = 30/4 = 7.5
Which is the population variance of the four numbers. We don’t calculate the first central moment because it will always be zero. The overall purpose of moments in machine learning are too tell us certain properties of a distribution such as the mean, time domain features, effective features, and how skewed the distribution is.
Variation or variance is also important in machine learning as it may appear in classification results, and helps to deduce joint distribution discrepancies. While discussing model accuracy and classification performance, we need to keep in mind the prediction errors, which include bias and variance, that will always be associated with any effective machine learning model. There will always be a slight difference in what our target samples and the source samples. These differences are called errors.
The goal of an analyst is not to eliminate errors but to reduce them. Bias is the difference between our actual and predicted values. Bias is the simple assumptions that our model makes about our data to be able to predict new data. When the Bias is high, assumptions made by our model are too basic, the model can’t capture the important features of our data. This means that our model hasn’t captured patterns in the training data and hence cannot perform well on the testing data too. If this is the case, our model cannot perform on new data and cannot be sent into production. This instance, where the model cannot find patterns in our training set and hence fails for both seen and unseen data, is called underfitting.
Variance is the very opposite of Bias. During training, it allows our model to see the data a certain number of times to find patterns in it. If it does not work on the data for long enough, it will not find patterns and bias occurs. On the other hand, if our model is allowed to view the data too many times, it will learn very well for only that data. It will capture most patterns in the data, but it will also learn from the unnecessary data present, or from the noise. We can define variance as the model’s sensitivity to fluctuations in the data.
Our model may learn from noise. This will cause our model to consider trivial features as important. High variance in a batch of training samples leads to a machine learning model overfitting. For any model, we have to find the perfect balance between Bias and Variance. This just ensures that we capture the essential patterns in our model while ignoring the noise present it in. This is called Bias-Variance Tradeoff. It helps optimize the error in our model and keeps it as low as possible. An optimized model will be sensitive to the patterns in our data, but at the same time will be able to generalize to new data.
Conditions for Joint Probability
Remember that joint probability is the probability of the intersection of two or more events written as p(A ∩ B). There are two conditions for joint probability as seen below:
One is that events X and Y must happen at the same time. For example, throwing two dice simultaneously.
The other is that events X and Y must be independent of each other. That means the
outcome of event X does not influence the outcome of event Y. For example throwing two dice.
If the following conditions are met, then P(A∩B) = P(A) * P(B).
Joint probability cannot be used to determine how much the occurrence of one event influences the occurrence of another event. Therefore the joint probability of X and Y (two dependent events) will be P(Y). The joint probability of two disjoint events will be 0 because both the events cannot happen together. For events to be considered dependent, one must have an influence over how probable another is. In other words, a dependent event can only occur if another event occurs first. For example, say you want to go on vacation at the end of next month, but that depends on having enough money to cover the trip.
You may be counting on a bonus, a commission, or an advance on your paycheck. It also most likely depends on you being given the last week of the month off to make the trip. For dependent events conditional probability is used instead over joint probability. An event is deemed independent when it isn’t connected to another event, or its probability of happening, or conversely, of not happening. For example, the color of your hair has absolutely no effect on where you work. Independent events don’t influence one another or have any effect on how probable another event is. Joint probability can also be used for multivariate classification problems.
Application in Machine Learning
Joint probability is one of the many probability formula’s that find use in machine learning. This is because probabilistic assumptions are made on uncertain data. This is extremely prevalent in pattern recognition algorithms and other approaches for classification. Pattern recognition is the process of recognizing patterns by using a machine learning algorithm, which involves the classification of images. Pattern recognition can be defined as the classification of data based on knowledge already gained or on statistical information extracted from patterns and/or their representation.
One of the important aspects of pattern recognition is its application potential. In a typical pattern recognition application, the raw data is processed and converted into a form that is amenable for a machine to use. Pattern recognition involves the classification and cluster of patterns. In classification, an appropriate class label is assigned to a pattern based on an abstraction that is generated using a set of training patterns or domain knowledge. Classification is used in supervised learning.
There are many different types of classification algorithms such as MI-EEG signal classification, LSTM-based EEG classification, Cross-subject EEG signal classification, and classification of motor imagery. Clustering generates a partition of the data which helps decision making, the specific decision-making activity of interest to us. Clustering is used in unsupervised learning. The patterns are made up of individual features, which can be continuous, discrete or even discrete binary variables, or sets of features evaluated together, known as a feature vector.
The biggest advantages are that this model will generate a classification of some confidence level for every data point and often reveals subtle, hidden patterns not readily seen with human intuition. Generally, the more feature variables the algorithm is programmed to check for and the more data points available for training, the more accurate it will be.
This applies whether the target domain or the source domain are labeled or unlabeled. Joint distribution also sets up the framework for transfer learning and deep transfers to adapt via a transfer component. Transfer learning is a machine learning method where a model developed for a task is reused as the starting point for a model on a second task. It is a popular approach in deep learning where pre-trained models are used as the starting point on computer vision and natural language processing tasks given the vast compute and time resources required to develop neural network models on these problems and from the huge jumps in skill that they provide on related problems.
Also Read: Overfitting vs Underfitting in Machine Learning Algorithms
Conclusion
In conclusion joint distribution is an important part of machine learning. This is mostly because of how important pattern recognition algorithms are in today’s world. They are used in speech recognition, speaker identification, multimedia document recognition (MDR), automatic medical diagnosis, and networks for feature extraction. It also helps to make AI smarter and faster. There are also other types of probability distributions used in machine learning such as conditional distributions and marginal distributions. More about the topic can be found on Stack Exchange which is a Q&A board for data science questions. Thank you for reading this article.
References
“Joint Distribution.” DeepAI, 17 May 2019, https://deepai.org/machine-learning-glossary-and-terms/joint-distribution. Accessed 12 Feb. 2023.
Lab, Intelligent Systems. “Basics of Joint Probability.” YouTube, Video, 6 Apr. 2020, https://youtu.be/CQS4xxz-2s4. Accessed 12 Feb. 2023.
Nerd, Random. “Probability Distribution.” Medium, 25 July 2019, https://medium.com/@neuralnets/probability-distribution-statistics-for-deep-learning-73a567e65dfa. Accessed 12 Feb. 2023.