Introduction
Naive Bayes probabilistic classifiers are one of the simplest machine learning algorithms, but it is still used today. It is based on the Bayes theorem and there exists an entire group of Naive Bayes classifiers. It is used today because it is still fast, accurate, and reliable, which allows it to work well with things like natural language processing and spam filtering. There exists one common principle among Bayes classifiers. That is that every pair of features must be independent from one another.
First off, in order to understand Naive Bayes classifiers better, we must first understand how the Bayes theorem works. However, to understand that we must first talk about probability and conditional probability.
Table of contents
- Introduction
- What Is Probability?
- What is Conditional Probability?
- What is Bayes Theorem?
- What is Bayes Theorem from a Machine Learning Perspective?
- Working of the Naive Bayes Algorithm
- Applications of Naive Bayes Classifier
- Advantages of Naive Bayes Classifier
- Disadvantages of Naive Bayes Classifier
- Conclusion
- References
Also Read: What is Joint Distribution in Machine Learning?
What Is Probability?
Uncertainty involves making decisions with incomplete information, and this is the way we generally operate in the world. Handling uncertainty is typically described using everyday words like chance, luck, and risk. Probability is a field of mathematics that gives us the language and tools to quantify the uncertainty of events and reason in a principled manner. For example, we can quantify the marginal probability of a fire in a neighborhood, a flood in a region, or the purchase of a product.
Probabilistic models can define relationships between variables and be used to calculate probabilities. The probability of an event can be calculated directly by counting all of the occurrences of the event, dividing them by the total possible occurrences of the event. The assigned probability is a fractional value and is always in the range between 0 and 1, where 0 indicates no probability and 1 represents full probability. Together, the probability of all possible events sums to the probability value one. There are certain types of probability, one such type is known as conditional probability.
What is Conditional Probability?
Conditional probabilities allow you to evaluate how prior information affects probabilities. For example, what is the probability of A given B has occurred? When you incorporate existing facts into the calculations, it can change the likelihood table of an outcome. Typically, the problem statement for conditional probability questions assumes that the initial event occurred or indicates that an observer witnesses it.
The goal is to calculate the chances of the second event under the condition that the first event occurred. This concept might sound complicated, but it makes sense that knowing an event occurred can affect the chances of another event. For example, if someone asks you, what is the likelihood that you’re carrying an umbrella? Wouldn’t your first question be, is it raining? Obviously, knowing whether it is raining affects the chances that you’re carrying an umbrella. Now that we have an understanding of conditional probability, we can move on to the Bayes theorem.
Also Read: What is Argmax in Machine Learning?
What is Bayes Theorem?
Bayes’ Theorem, named after 18th-century British mathematician Thomas Bayes, is a mathematical formula for determining conditional probability. Remember that conditional probability is the likelihood of an outcome occurring, based on a previous outcome having occurred in similar circumstances. Bayes’ theorem provides a way to revise existing predictions or theories given new or additional evidence. In finance, Bayes’ Theorem can be used to rate the risk of lending money to potential borrowers. The theorem is also called Bayes’ Rule or Bayes’ Law and is the foundation of the field of Bayesian statistics. Applications of Bayes’ Theorem are widespread and not limited to the financial realm.
For example, Bayes’ theorem can be used to determine the accuracy of medical test results by taking into consideration how likely any given person is to have a disease and the general accuracy of the test. Bayes’ theorem relies on incorporating prior probability distributions in order to generate posterior probabilities. Prior probability, in Bayesian statistical inference, is the probability of an event occurring before new data is collected. In other words, it represents the best rational assessment of the probability of a particular outcome based on current knowledge of conditions before an experiment is performed.
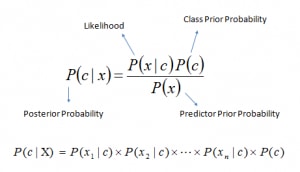
Posterior probability is the revised probability of an event occurring after taking into consideration the new information. Posterior probability is calculated by updating the prior probability using Bayes’ theorem. In statistical terms, the posterior probability is the probability of event A occurring given that event B has occurred. Bayes’ Theorem thus gives the probability of an event based on new information that is, or may be, related to that event. The formula can also be used to determine how the probability of an event occurring may be affected by hypothetical new information, supposing the new information will turn out to be true. Today, the theorem has become a useful element in machine learning as seen in Naive Bayes classifiers.
What is Bayes Theorem from a Machine Learning Perspective?
Although it is a powerful tool in the field of probability, Bayes Theorem is also widely used in the field of machine learning. Including its use in a probability framework for fitting a model to a training dataset, referred to as maximum a posteriori or MAP for short, and in developing models for classification predictive modeling problems such as the Bayes Optimal Classifier and Naive Bayes. Classification is a predictive modeling problem that involves assigning a label to a given input feature data sample.
The problem of classification predictive modeling can be framed as calculating the maximum conditional probability of a class probability label given a data sample. For example we can have the following, P(class|data) = (P(data|class) * P(class)) / P(data). Where P(class|data) is the probability of class given the provided data. This calculation can be performed for each class in the problem and the class that is assigned the largest probability can be selected and assigned to the input feature array data.

In practice, it is very challenging to calculate full Bayes Theorem for classification. The priors for the class and the data are easy to estimate from a training dataset, if the dataset is suitability representative of the broader problem. The conditional probability of the observation based on the class P(data|class) is not feasible unless the number of examples is extraordinarily large.
Working of the Naive Bayes Algorithm
The solution to using Bayes Theorem for a conditional probability classification model is to simplify the calculation. The Bayes Theorem assumes that each class input variable is dependent upon all other class variables. This is a cause of complexity in the calculation. We can remove this strong assumption and consider each input variable as being independent from each other. This changes the model from a dependent conditional probability model to an independent conditional probability model and dramatically simplifies the calculation.
This means that we calculate P(data|class) for each input variable separately and multiply the results together. This simplification of Bayes Theorem is common and widely used for classification predictive modeling problems and is generally referred to as the Naive Bayes algorithm. There are three types of Naive Bayes models. These are the Gaussian model, the Multinomial model, and the Bernoulli model. The Gaussian model assumes that features follow a normal distribution. A normal distribution means if predictors take continuous values instead of discrete features, then the model assumes that these values are sampled from the Gaussian distribution.
The Multinomial Naive Bayes classifier is used when the data is multinomial distributed. It is primarily used for document classification problems, which means deciding if a particular document belongs to a specific category such as sports, politics, or education. The classifier uses the frequency tables of words for the predictors.
The Bernoulli classifier works similar to the Multinomial classifier, but the predictor variables are the independent Booleans variables. Such as if a particular word is present or not in a document. This model is also famous for document classification tasks.
Applications of Naive Bayes Classifier
Naïve Bayes algorithm is a supervised learning algorithm. It is based on Bayes theorem and is used for solving classification problems. It is mainly used in text classification that includes a high-dimensional training dataset. Naive Bayes Classifier is one of the simple and most effective Classification algorithms which helps in building the fast machine learning models that can make quick predictions. It is a probabilistic classifier, which means it predicts on the basis of the probability of an object.
It can also be used in medical data classification, credit scoring, and even real time predictions. Email services (like Gmail) use this algorithm to figure out whether an email is a spam or not. Its assumption of basic feature independence, and its effectiveness in solving multi-class problems, makes it perfect for performing Sentiment Analysis.
Sentiment Analysis refers to the identification of positive or negative sentiments of a target group. Collaborative Filtering and the Naive Bayes algorithm work together to build recommendation systems. These systems use data mining and machine learning to predict if the user would like a particular resource or not.
Advantages of Naive Bayes Classifier
The Naive Bayes classifier is a popular algorithm, and thus it has many advantages. Some include:
- This algorithm works very fast and can easily predict the actual class of a test dataset. It is able to move fast because there are no iterations.
- You can use it to solve multi-class prediction problems as it’s quite useful with them. This is the problem of classifying instances into one of three or more classes.
- If you have categorical input variables, the Naive Bayes algorithm performs exceptionally well in comparison to numerical variables.
- It can be used for Binary and Multi-class Classifications.
- It effectively works in Multi-class predictions as compared to other algorithms.
- It is the most popular choice for text classification problems. Text classification is a supervised learning problem, which categorizes text/tokens into the organized groups, with the help of Machine Learning & Natural Language Processing.
- It is easy to implement in Python. There are five steps to follow when implementing it, these are the data pre-processing step, fitting Naive Bayes to the training set, predicting the test result, test the accuracy of the result, and finally visualize the test set result.
- Naive Bayes gives useful and intuitive outputs such as mean values, standard deviation and joint probability calculation for each feature vector and class.
- Naive Bayes scales linearly which makes it a great candidate for large setups.
- Naive Bayes uses very little resources (Ram & Cpu) compared to other algorithms.
- If your data has noise, irrelevant features, outlier values etc., no worries, Naive Bayes thrives in such situations and its prediction capabilities won’t be seriously affected like some of the other algorithms.
- Naive Bayes’ simplicity comes with another perk. Since it’s not sensitive to noisy features that are irrelevant these won’t be well represented in Naive Bayes Model. This also means that there is no risk of overfitting.
Disadvantages of Naive Bayes Classifier
There are also some disadvantages, as with most machine learning algorithms, of using the Naive Bayes classifier. Some include:
- If your test data set has a categorical variable of a category that wasn’t present in the training data set, the Naive Bayes model will assign it zero probability and won’t be able to make any predictions in this regard. This phenomenon is called ‘Zero Frequency,’ and you’ll have to use a smoothing technique to solve this problem.
- This algorithm is also notorious as a lousy estimator. So, you shouldn’t take the probability outputs of ‘predict_proba’ too seriously.
- It assumes that all the features are independent. While it might sound great in theory, in real life, you’ll hardly find a set of independent features.This also makes it unable to learn any relationships between features.
- Since Naive Bayes is such a quick and dirty method and it avoids noise so well this also might mean shortcomings. Naive Bayes processes all features as independent and this means some features might be processed with a much higher bias than you’d wish.
- Naive Bayes Classifier is strictly a classification algorithm and can’t be used to predict continuous numerical value, hence no regression with Naive Bayes Classifier.
Also Read: Top Data Science Interview Questions and Answers
Conclusion
Despite its limitations Naive Bayes is still used in many situations today. Bayes Theorem can be used in calculating conditional and Bayesian probabilities and it is used in machine learning. Other cases not covered here include Bayesian optimization and Bayesian belief networks. However, developing classifier models is the most used case of the Bayes theorem when it comes to machine learning. Thank you for reading this article.
References
Gandhi, Rohith. “Naive Bayes Classifier.” Towards Data Science, 17 May 2018, https://towardsdatascience.com/naive-bayes-classifier-81d512f50a7c. Accessed 11 Feb. 2023.
Starmer, StatQuest with Josh. “Naive Bayes, Clearly Explained!!!” YouTube, Video, 3 June 2020, https://youtu.be/O2L2Uv9pdDA. Accessed 11 Feb. 2023.