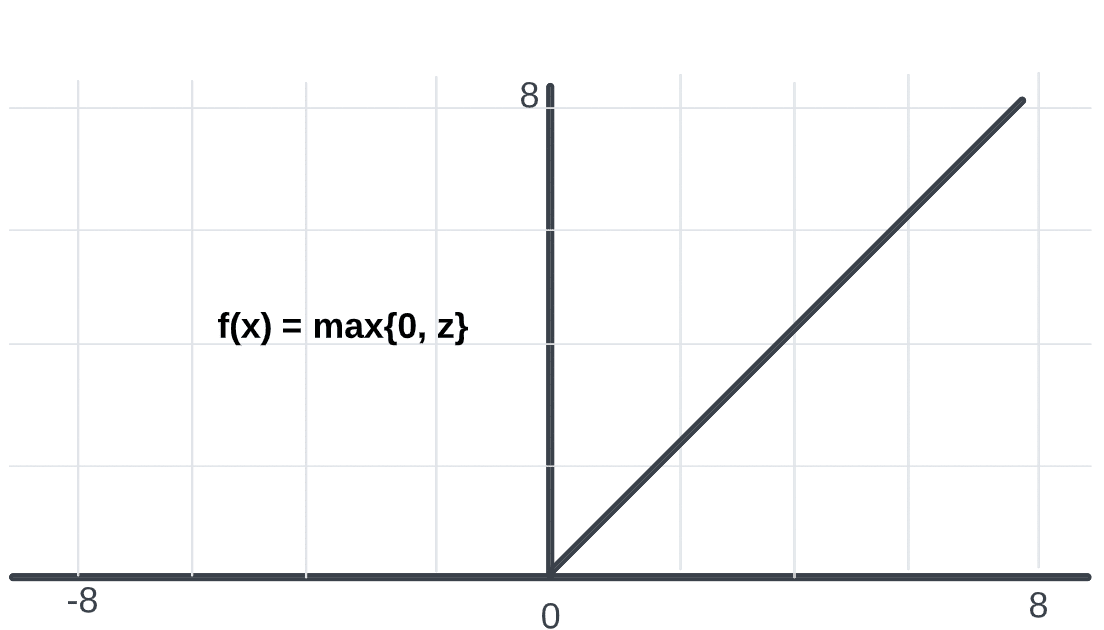Introduction:
There is no doubt that activation functions play a significant role in the ignition of the hidden nodes within neural networks and deep learning in order to produce a higher-quality output. It is the purpose of the activation function to introduce the property of non-linearity into the model in order to achieve the intended purpose.
An artificial neural network’s activation function determines the output of a node given an input or set of inputs. Integrated circuits can be viewed as digital networks of activation functions that can be turned on or off based on input.
Table of contents
What is ReLU
The rectified linear activation function or ReLU for short is a piecewise linear function that will output the input directly if it is positive, otherwise, it will output zero. It has become the default activation function for many types of neural networks because a model that uses it is easier to train and often achieves better performance. The other variants of ReLU include Leaky ReLU, ELU, SiLU, etc., which are used for better performance in some tasks.
There was a time when the sigmoid and tanh were monotonous, differentiable, and more popular activation functions. Over time, however, these functions suffer saturation, and as a result, vanishing gradients become more and more problematic as the time goes on. To overcome this issue, the Rectified Linear Unit (ReLU) is the most popular activation function that can be used to solve the problem.
It is important to recognize that in a neural network, the activation function is responsible for converting the weighted sum of the inputs from the nodes into an activation for the nodes or outputs for that input in the network.
The activation function was first introduced to a dynamical network by Hahnloser et al. in the year 2000, with strong biological motivations and mathematical arguments for its use. There is a new activation function that has been demonstrated for the first time in 2011 to be capable of enabling the better training of deeper networks compared to the activation functions that have previously been widely used, such as the logistic sigmoid (inspired by probability theory and logistic regression) and its more practical counterpart, hyperbolic tangent.
Activation functions for deep neural networks are dominated by rectifiers as of 2017. Rectified linear units (ReLUs) are units that employ the rectifier.
There are several reasons why ReLU has not been used more frequently before, even though it is one of the best activation functions. There was a reason for this, which was because it was not differentiable at the 0 point. It was common for researchers to use differentiable functions such as sigmoid and tanh in their studies. It has been found, however, that ReLU is the best activation function for deep learning because of its simplicity and ease of use.
There are no points in the ReLU activation function where it is not differentiable, except at 0. Whenever the function has a value greater than 0, we just consider the maximum value of the function. As a result, the following function can be used:
f(x) = max{0, z}
if input > 0:
return input
else:
return 0;
Negative values default to zero, and positive numbers are taken up to their maximum. In order to compute the backpropagation of neural networks, it is relatively easy to differentiate the ReLU for the computation of the back propagation. Only one assumption will be made, and that is the derivative at the point 0, which will also be considered to be zero as well. Slope is the value that can be derived from the derivative of a function. The slope for negative values is 0.0, and the slope for positive values is 1.0.

Source: Wiki
Also Read: How to Use Linear Regression in Machine Learning.
The main advantages of the ReLU activation function are:
1. Convolutional layers and deep learning: They are the most popular activation functions for training convolutional layers and deep learning models.
2. Computational Simplicity: The rectifier function is trivial to implement, requiring only a max() function.
3. Representational Sparsity: An important benefit of the rectifier function is that it is capable of outputting a true zero value.
4. Linear Behavior: A neural network is easier to optimize when its behavior is linear or close to linear.
However, with the Rectified Linear Unit, all negative values become zero immediately, which hinders the model’s ability to fit or train properly from the data.
ReLU activation function turns any negative input into zero immediately in the graph, which adversely affects the resulting graph by not mapping the negative values appropriately. By using the various variants of the ReLU activation function, like the Leaky ReLU and other variants, this can easily be fixed.
Limitations of Sigmoid and Tanh Activation Functions
The neural network is made up of layers of nodes and is designed to learn how to map examples of inputs to outputs based on the inputs.
In the case of a given node, the inputs are multiplied by the weights in the node and the sum of the weights is computed for that node. This value can be referred to as the summed activation of the nodes in the network. Using an activation function, the summed activation is transformed into the specific output or “activation” of the node by applying the activation function to the summed activation.
A linear activation function is the simplest type of activation function, where no transform is applied at all, so the function is referred to as a linear activation. It is very easy to train a network that consists only of linear activation functions, however, it cannot learn complex mapping functions. In a network that predicts a quantity (e.g. a regression problem), linear activation functions are still used in the output layer of the network.
Nodes can learn more complex structures in the data if they use nonlinear activation functions as they allow them to learn more complex structures in the data. As far as nonlinear activation functions are concerned, two widely used nonlinear activation functions are the sigmoid and hyperbolic tangent activation functions.
For neural networks, the sigmoid activation function, also known as the logistic function, is traditionally one of the most popular activation functions. The input to the function is transformed into a value between 0.0 and 1.0 depending on the size of the input. Whenever an input value is much bigger than 1.0, it is transformed to the value 1.0, like when an input value is much smaller than 0.0, it is snapped to 0.0. As far as the shape of the function is concerned, for all possible inputs, the curves are S-shaped, ranging from zero to 0.5 to 1.0.
As the name suggests, the hyperbolic tangent function, or tanh for short, is a similar shaped nonlinear activation function that outputs values between -1.0 and 1.0.
Sigmoid and tanh functions both suffer from the general problem of saturating at certain point in their computation. For tanh and sigmoid, this means that large values will be rounded up to 1.0 while small values will be rounded down to -1 or 0. As a result, these functions are only very sensitive when their mid-points of their inputs are changed, such as 0.5 for the sigmoid and 0.0 for the tanh functions.
It should be noted that the limited sensitivity and saturation of the function happen regardless of whether or not the summation of activation is contained within the input node that is provided or not. When the learning algorithm gets saturated, it becomes difficult for it to continue adapting the weights in order to improve the performance of the model once it has become saturated.
In conclusion, as the hardware capability of the GPUs increased, very deep neural networks using sigmoid or Tanh activation functions were unable to be trained as easily due to the limited capabilities of the GPU.
When using these nonlinear activation functions in large networks, gradient information is not received in layers deep in the network. When there is an error, it is propagated back through the network and the weights of the network are updated as a result. Given the derivative of the activation function chosen, the amount of error that is propagated through each additional layer through which it is propagated decreases dramatically with each additional layer. This problem is known as the vanishing gradient problem, and it prevents deep (multilayered) networks from being able to learn effectively as a result.
There is no doubt that neural networks are able to learn complex mapping functions thanks to the use of nonlinear activation functions, but deep learning algorithms are not able to take advantage of these functions.
Also Read: Introduction to Long Short Term Memory (LSTM).
Applications of ReLU
ReLU in Image Recognition and Computer Vision
Rectified Linear Units (ReLU) have been a cornerstone in the field of image recognition and computer vision, particularly within the framework of Convolutional Neural Networks (CNNs). By introducing non-linearity without impacting the receptive fields of convolution layers, ReLU plays a crucial role in tasks such as object detection, image segmentation, and facial recognition. The zeroing property of ReLU on negative inputs is particularly beneficial in these cases, as it helps to mitigate the vanishing gradient problem, thereby enabling the network to learn complex, hierarchical patterns within images. ReLU’s simple and efficient computation process significantly accelerates training, facilitating the construction and optimization of deep networks capable of recognizing intricate visual details.
Applying ReLU in Natural Language Processing
ReLU and its variants have found widespread application in Natural Language Processing (NLP) tasks, employed within the architecture of Recurrent Neural Networks (RNNs) and Transformer models. ReLU’s inherent characteristic of assigning zero to negative inputs introduces beneficial non-linearity, which aids in capturing the intricate structures of languages. It alleviates the vanishing gradient issue, enabling efficient training of deep and complex models on voluminous textual data. This proves instrumental in a variety of NLP tasks such as sentiment analysis, machine translation, and text summarization, where the quick training facilitated by ReLU helps models to deliver accurate results in a time-efficient manner.
Using ReLU for Speech Recognition Systems
In the domain of speech recognition, ReLU activation functions offer a range of advantages. The ability of ReLU to introduce non-linearity into the network and mitigate the vanishing gradient problem is of significant value in building robust speech recognition systems. Deep neural networks utilizing ReLU functions are often employed to extract intricate features from raw audio signals. The computational efficiency of ReLU, which simplifies the forward propagation process by zeroing out negative inputs, is especially beneficial in real-time speech recognition scenarios. This simplification speeds up computations, enhances system responsiveness, and leads to superior overall performance.
ReLU in Neural Networks for Self-driving Cars
ReLU is an integral part of the neural networks that power self-driving cars. These autonomous vehicles rely heavily on CNNs, which utilize ReLU for its computational efficiency and ability to mitigate the vanishing gradient problem. These networks process the massive volumes of visual data collected by the vehicle’s sensors to identify objects, interpret traffic signals, and make driving decisions. In such real-time applications, the computational efficiency of ReLU is crucial. The non-linear characteristics of ReLU help these networks to recognize complex patterns and make accurate predictions, contributing to safer and more reliable autonomous navigation.
The Role of ReLU in Healthcare and Medical Diagnostics
The healthcare sector has embraced ReLU for its potential in medical diagnostics, including tasks like disease detection, medical image analysis, and patient data interpretation. ReLU’s characteristics are particularly suited for processing medical imaging data where it’s crucial to detect subtle patterns. By reducing the vanishing gradient problem, ReLU enables the training of deep learning models on large datasets of patient records and medical images. These models, powered by ReLU, are then capable of identifying the minutest abnormalities and predicting potential health risks, aiding in early disease diagnosis and personalized patient care. The computational efficiency of ReLU contributes to faster results, which is of paramount importance in time-critical medical scenarios.
Conclusion
Rectified Linear Unit (ReLU) function is a crucial component in the construction and success of many deep learning models. It has become the default activation function for many types of neural networks because it effectively mitigates the vanishing gradient problem. This problem, common in traditional activation functions like the sigmoid or hyperbolic tangent, causes the gradients to become increasingly small as the network learns, slowing down the learning process or causing it to halt altogether. The simplicity of ReLU, only activating when the input is positive, allows for faster and more efficient training of large neural networks.
ReLU is also computationally efficient due to its simplicity. It requires less computational power to apply compared to other non-linear functions, which is advantageous when dealing with large scale, high dimensional data. The function essentially carries out a threshold operation, assigning a value of zero to all negative inputs, and letting positive values pass through unaffected. This characteristic leads to the development of sparse representations with fewer active neurons, further enhancing computational efficiency and aiding generalization.
Despite its advantages, ReLU is not without drawbacks. One such issue is the “dying ReLU” problem, where some neurons can become inactive and only output zero – essentially leading to a portion of the model that is not learning. Variants such as the Leaky ReLU and Parametric ReLU have been proposed to mitigate this issue, introducing a small, positive gradient for negative inputs, thereby keeping the neurons ‘alive’ and ensuring they continue to learn.
In the broader context, the emergence and popularity of ReLU underscore the evolving nature of deep learning research. As the field continues to advance, it’s likely that new activation functions will be proposed and existing ones will be refined further. This reflects the overarching goal of deep learning – to continually enhance the effectiveness and efficiency of artificial neural networks to better mimic and possibly surpass the information processing capabilities of the human brain.
References
Das, Himansu, et al. Deep Learning for Data Analytics: Foundations, Biomedical Applications, and Challenges. Academic Press, 2020.
Vasudevan, Shriram K., et al. Deep Learning: A Comprehensive Guide. CRC Press, 2021.