Introductory Overview of the Sigmoid Function
The Sigmoid function, is often denoted by the mathematical function –
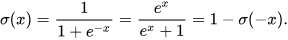
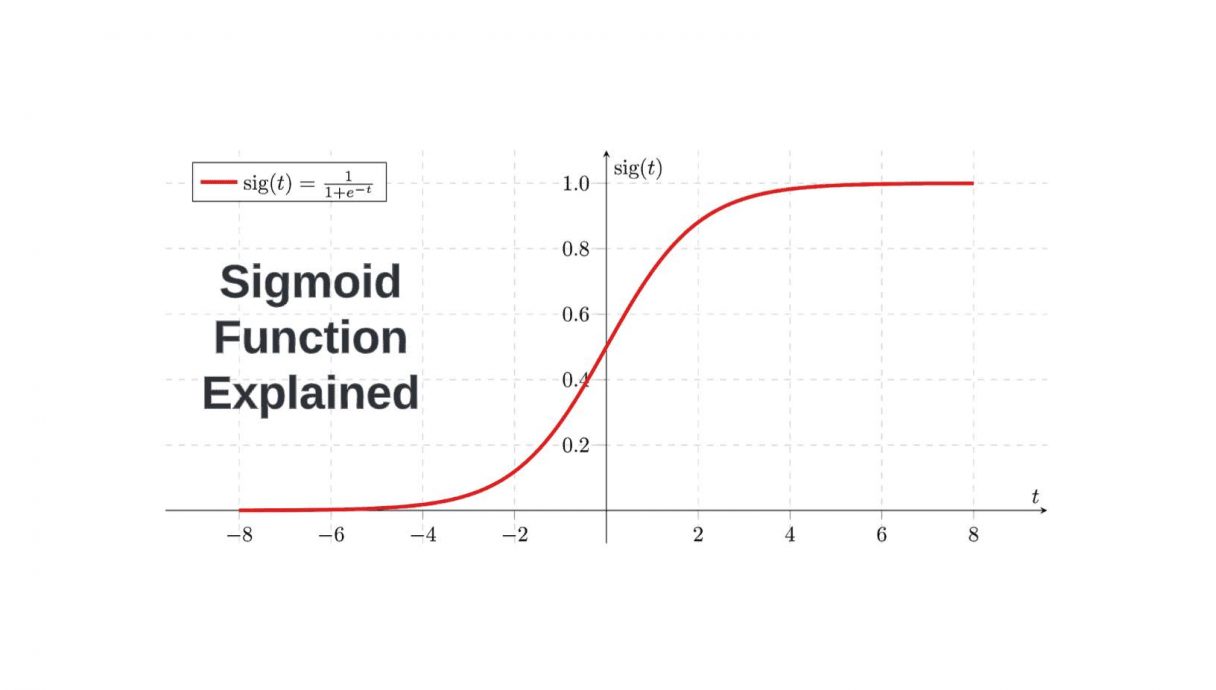
It serves as a crucial element in various computational fields, particularly machine learning and statistics. It maps any input value into a range between 0 and 1, providing a way to normalize or ‘squash’ numbers. This bounded range makes it useful in calculations involving probabilities.
The function exhibits an S-shaped curve when plotted on a graph, known as a sigmoid curve. The shape of this curve implies that changes in the output are gradual and nonlinear. The curve is steeper in the middle, indicating greater sensitivity to changes in input values close to zero.
The Sigmoid function has found extensive use in logistic regression, neural networks, and other machine learning algorithms. It helps in transforming complex, non-linear relationships in data to make them more interpretable and manageable for computation. The function is also useful in producing probabilities in binary decision problems.
Table of contents
- Introductory Overview of the Sigmoid Function
- Understanding the Sigmoid Function
- Characteristics and Qualities of the Sigmoid Function
- The Role of the Sigmoid Function as a Squashing Mechanism
- Utilizing Sigmoid in Neural Network Activation
- Distinguishing Between Linear and Non-Linear Classifications
- The Significance of the Sigmoid Function in Neural Computing
- Use Cases for the Sigmoid Function
- Final Thoughts on the Sigmoid Function
- References
Understanding the Sigmoid Function
The sigmoid function is a monotonic function, meaning that it either consistently increases or decreases, but does not do both. The function takes an input from the set of all real numbers and maps it to an output range between 0 and 1.
Its non-linear characteristics make it quite distinct from linear functions. The bounded output range allows it to act as a squashing function, effectively compressing a wide range of input values to a fixed and narrow range.
In machine learning, the Sigmoid function is often employed as an activation function in neural network models, including but not limited to binary classification tasks. While linear regression models are well-suited for predicting numerical values, the non-linear nature of the Sigmoid function makes it ideal for scenarios where the outcome needs to be a probability value, such as classification problems. It serves as an alternative to other activation functions like the softmax function, especially when the neural network has to distinguish between just two classes in its output layer.
When it comes to the computational aspects of machine learning, derivatives play a crucial role, especially during the optimization phase. In this context, the Sigmoid function offers an advantage. Its first derivative is relatively simple to compute and can be expressed in terms of the function itself.
This property facilitates the backpropagation process in neural networks, making it computationally efficient. Furthermore, the Sigmoid function bears a resemblance to the normal distribution, although it is not a probability distribution itself, which can be beneficial in statistical interpretations of neural network models.
Characteristics and Qualities of the Sigmoid Function
The Sigmoid function is characterized by its smooth, “S”-shaped curve, making it differentiable at all points. This property is crucial when solving optimization problems, as the derivative function helps in computing gradients for backpropagation in machine learning models. Its bounded output range between 0 and 1 is particularly advantageous for interpreting the output as probabilities.
Despite these strengths, it is essential to note that the Sigmoid function is not zero-centered; its output does not distribute around zero. This characteristic contrasts with other common activation functions like the Hyperbolic function or the identity function, and it can lead to gradients that are not zero-centered, affecting the model’s learning dynamics.
While the Sigmoid function is widely used as a neural network activation function, it has its shortcomings. One of the most significant issues is the “vanishing gradient” problem. When the input values are either very large or very small, the Sigmoid function’s derivative approaches zero.
This causes neuron activations to become almost constant, leading to difficulties in adjusting the layers of neurons during the learning process. Sigmoid neurons can suffer from this problem more than biological neurons or input neurons, limiting their efficiency in specific machine learning models.
Computational expense is another factor to consider when using the Sigmoid function. The function relies on exponentiation, a computational operation that can be taxing on resources. This is a crucial aspect in scenarios requiring real-time predictions or when computational constraints are present.
Alternative activation functions like the Swish function or the arctangent function might be considered in such cases. Also, for multi-class classification problems, one might opt for other functions like the error function or even an exponential model, which may offer more flexibility and better performance.
Also Read: What is Univariate Linear Regression? How is it Used in AI?
The Role of the Sigmoid Function as a Squashing Mechanism
The Sigmoid function serves as a powerful tool for squashing high-dimensional, unbounded input data into a low-dimensional, bounded space between 0 and 1. In the realm of Activation Functions in Neural Networks, this property is invaluable for tasks like binary classification. The activation potential of the sigmoid unit can transform an input vector into an output vector that is easier to manage and interpret.
This function aids in stabilizing the numerical computations within the machine learning algorithms by normalizing the output values. This is particularly beneficial in the initial layers of neural networks where it helps contain the values, ensuring they don’t reach extreme highs or lows that could cause computational instability.
On the flip side, the squashing property of the Sigmoid function can also be its Achilles’ heel, particularly when dealing with complex tasks in deep learning architectures. When the function squashes the input data, it can result in the notorious vanishing gradient problem.
In this situation, the gradients during the backpropagation become so small that they hardly contribute to the weight update, making it difficult for the network to learn effectively. This issue becomes especially challenging for negative input values, as the gradients near zero can slow down the training of the model substantially.
Due to these limitations, researchers and practitioners have developed and adopted alternative activation functions that try to mitigate these issues. One such function is the ReLU (Rectified Linear Unit) and its variant, the Leaky ReLU Function, which aim to solve the vanishing gradient issue.
These alternatives allow for logical adjustment during the learning process without contracting the gradients as severely as the Sigmoid function. While the Sigmoid function is still used for specific tasks, and especially for binary activation functions, its limitations have led the field to explore various alternatives for different application needs.
Utilizing Sigmoid in Neural Network Activation
The Sigmoid function is one of the earliest activation functions used in neural networks. In a neural network, activation functions are responsible for transforming the summed weighted input from the node into the output for that node. The Sigmoid function was widely adopted because it is nonlinear, differentiable, and easy to understand.
In binary classification problems, the Sigmoid activation is particularly useful in the output layer. It can turn arbitrary real-valued numbers into probabilities, which are easier to interpret. This has made it the go-to activation function in logistic regression models as well.
While it remains popular in specific types of problems, the Sigmoid function has been somewhat superseded by other activation functions like ReLU, which address some of the Sigmoid function’s shortcomings. ReLU and its variants often provide better performance in deep networks, thanks to their ability to mitigate the vanishing gradient problem.
Distinguishing Between Linear and Non-Linear Classifications
Linear classification involves finding a linear boundary to separate different classes in the feature space. For example, in two dimensions, this boundary could be a straight line. Non-linear classification involves a boundary that is not a straight line and can take on more complex shapes.
The Sigmoid function, being a nonlinear function, enables the creation of non-linear decision boundaries. This is essential for handling real-world data that often is not easily separable by a linear boundary. Non-linear classifiers are capable of capturing the intricate patterns in such data.
Many machine learning algorithms offer the flexibility to choose between linear and non-linear decision boundaries. Algorithms like SVM (Support Vector Machine) can be configured to work as both linear and non-linear classifiers. The choice of linear vs. non-linear separability ultimately depends on the nature of the data and the problem at hand.
The Significance of the Sigmoid Function in Neural Computing
In the realm of neural computing, the Sigmoid function plays a vital role as an activation function. It helps neural networks deal with non-linearity in the data. The function is especially relevant in architectures like feedforward neural networks and backpropagation algorithms where gradient-based optimization is performed.
The Sigmoid function has historically been vital in the development of neural networks. It allowed the networks to learn from the error gradients during the training phase, contributing to more precise models.
Despite its wide usage, it’s essential to note that the Sigmoid function is not always the best choice for all layers in deep neural networks. Its limitations, such as the vanishing gradient problem, have made researchers and practitioners explore alternative activation functions.
Use Cases for the Sigmoid Function
In practical applications, the Sigmoid function is commonly employed in logistic regression, a statistical method for modeling binary outcomes. Beyond that, it’s used in artificial neural networks for binary classification problems. The Sigmoid function is also seen in other disciplines like economics for modeling growth rates and in physics for phenomena that exhibit saturation.
In the realm of natural language processing, the function is used for sentiment analysis and sequence prediction tasks. It also finds application in image recognition tasks, where it helps to classify objects into specific categories.
Although its utility is widespread, the Sigmoid function is not a one-size-fits-all solution. Different activation functions, like the hyperbolic tangent (tanh) or ReLU, might offer better performance depending on the specific requirements of a project.
This Python code example that simulates a real-life application of the sigmoid function in logistic regression for binary classification. We’ll use a dataset containing hours of study and corresponding pass/fail outcomes for a hypothetical exam.
First, let’s install the necessary libraries:
pip install numpy matplotlib scikit-learn
import numpy as np
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
# Hypothetical dataset: hours_studied vs. pass/fail (1: passed, 0: failed)
hours_studied = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]).reshape(-1, 1)
passed_exam = np.array([0, 0, 0, 0, 1, 1, 1, 1, 1, 1])
# Train a logistic regression model
model = LogisticRegression()
model.fit(hours_studied, passed_exam)
# Define the sigmoid function
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# Plotting
plt.figure(figsize=(9, 6))
# Scatter plot of the data
plt.scatter(hours_studied, passed_exam, color='blue', label='Real data')
# Plot the sigmoid curve
x_test = np.linspace(-2, 12, 300)
y_test = sigmoid(model.intercept_ + model.coef_ * x_test)
plt.plot(x_test, y_test, label='Sigmoid curve', color='red')
# Annotate the plot
plt.title('Sigmoid Function in Logistic Regression')
plt.xlabel('Hours Studied')
plt.ylabel('Passed Exam')
plt.legend()
plt.show()
# Make predictions
new_hours_studied = np.array([4.5]).reshape(-1, 1)
prediction = model.predict(new_hours_studied)
probability = sigmoid(model.intercept_ + model.coef_ * 4.5)[0][0]
print(f"Prediction: {'Passed' if prediction[0] == 1 else 'Failed'}")
print(f"Probability of passing: {probability:.2f}")In this example:
hours_studiedandpassed_examserve as our features and labels, respectively.- We use scikit-learn’s
LogisticRegressionto fit a model to our data. - The
sigmoidfunction is used to transform the logistic regression output into a probability. - We plot the real data along with the sigmoid curve to visualize how well it fits.
- Finally, we make a prediction for a student who studied 4.5 hours and show the probability of passing the exam.
This demonstrates a real-life application of the sigmoid function in the context of education and predictive analytics.
Also Read: Machine Learning For Kids: Python Functions.
Final Thoughts on the Sigmoid Function
The Sigmoid function has been a cornerstone in the field of machine learning and neural networks for several decades. Its characteristics, like the bounded output and smooth gradient, have made it a popular choice for many types of machine learning algorithms.
Despite its popularity, it’s crucial to acknowledge its limitations, such as the vanishing gradient problem and computational inefficiency in certain contexts. These limitations have led to the development of other activation functions designed to address these issues.
As technology progresses, newer activation functions may take the spotlight. However, the Sigmoid function will continue to be an essential tool in the toolkit of machine learning practitioners and data scientists, particularly for specific types of problems where its characteristics are most suited.
References
Das, Sibanjan, and Umit Mert Cakmak. Hands-On Automated Machine Learning: A Beginner’s Guide to Building Automated Machine Learning Systems Using AutoML and Python. Packt Publishing Ltd, 2018.
Networks, International Workshop on Artificial Neural. From Natural to Artificial Neural Computation: International Workshop on Artificial Neural Networks, Malaga-Torremolinos, Spain, June 7-9, 1995 : Proceedings. Springer Science & Business Media, 1995.
Satoh, Shin’ichi, et al. Advances in Multimedia Modeling: 14th International Multimedia Modeling Conference, MMM 2008, Kyoto, Japan, January 9-11, 2008, Proceedings. Springer Science & Business Media, 2007.